Lesson 8 – Prisms and Total Internal Reflection

Posted on: Monday, April 4th, 2022  In: Learning Optics with Austin

Besides lenses and mirrors, prisms are another group of common optical elements. White light that enters a prism leaves as many different colors due to the different refractive indexes of each color’s wavelength (a topic that will be covered in further depth in the next post). Besides refracting white light, prisms have another useful property that can result in 100% reflectivity (no exaggeration!). A reminder (from How Does Light Travel? Part I: Diffraction and Reflection) that reflectivity is the percentage of light that is reflected off a surface. Even with the most expensive coatings and smoothest surfaces, even mirrors cannot match the 100% reflectivity characteristic of prisms. How is it that prisms can surpass mirrors in reflectivity?

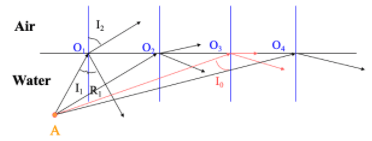
Total Internal Reflection Diagram

Total internal reflection is the property of prisms resulting in 100% reflectivity. While the conditions of total internal reflection are relatively straightforward, the math behind the phenomenon is a bit more involved. The diagram above shows two mediums, glass and air in which light must travel through. We set n₁ to be the refractive index of glass and n₂ to be the refractive index of air. A reminder (from How Does Light Travel? Part II: Refraction) that the higher the refractive index, the greater the “bending” of light. The first condition of total internal refraction is that n₁ > n₂, of which is the case in the diagram. The second condition is that the incidence angle (I₁) must be greater than the critical angle (I₀). The critical angle is the angle at which total internal reflection occurs, which in the diagram, would be I₄. Brace yourselves for a little math!

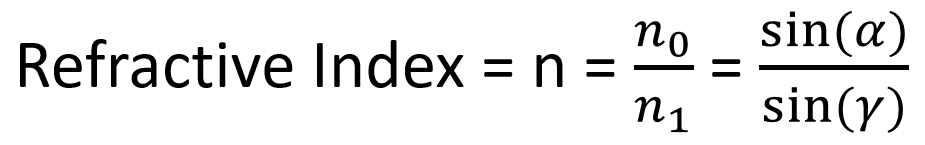
Refractive Index Equation

Using the relationship sin(I₁) / sin(I₂) = n₂ / n₁ mentioned in How Does Light Travel? Part II: Refraction (which also happens to be Snell’s Law: n₁ sin(I₁) = n₂ sin(I₂) rearranged), we can see from the diagram that I₂ can at most be 90 degrees. This is the point in which the refracted ray of light is parallel to the surface. The I₁ when I₂ is 90 degrees is the critical angle at which total internal reflection occurs. Since I₂ must always be less than or equal to 90 degrees (think about why to check your understanding), the most that sin(I₂) could be is 1 (since I₂ cannot be negative, the least it could be is 0 and sin(0) = 0 while sin(90^o) = 1). We can thus rewrite sin(I₁) / sin(I₂) = n₂ / n₁ as sin(I₁) = n₂ / n₁ where I₁ is the critical angle that can be calculated from sin^-1(n₂ / n₁).

Total Internal Reflection

After all this math, you might be wondering- why should I care? Remember that the incidence angle being greater than the critical angle is the second condition of total internal reflection. This property is what gives prisms 100% reflectivity, which is a feat even mirrors cannot achieve. By taking advantage of this property, you can save a lot of money and simplify the design of the optical system you are designing!

Next: Lesson 9 – Light Waves

About Austin

Comments are closed.